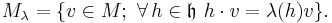Category O
Category O (or category  ) is a mathematical object in representation theory of semisimple Lie algebras. It is a category whose objects are certain representations of a semisimple Lie algebra and morphisms are homomorphisms of representations.
) is a mathematical object in representation theory of semisimple Lie algebras. It is a category whose objects are certain representations of a semisimple Lie algebra and morphisms are homomorphisms of representations.
Contents |
Introduction
Assume that  is a (usually complex) semisimple Lie algebra with a Cartan subalgebra
is a (usually complex) semisimple Lie algebra with a Cartan subalgebra  ,
,  is a root system and
is a root system and 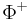 is a system of positive roots. Denote by
is a system of positive roots. Denote by 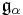 the root space corresponding to a root
the root space corresponding to a root 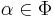 and
and 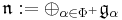 a nilpotent subalgebra.
a nilpotent subalgebra.
If  is a
is a  -module and
-module and 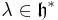 , then
, then 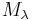 is the weight space
is the weight space
Definition of category O
The objects of category O are  -modules
-modules  such that
such that
 is finitely generated
is finitely generated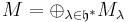
 is locally
is locally 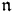 -finite, i.e. for each
-finite, i.e. for each 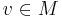 , the
, the 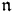 -module generated by
-module generated by  is finite-dimensional.
is finite-dimensional.
Morphisms of this category are the  -homomorphisms of these modules.
-homomorphisms of these modules.
Basic properties
- Each module in a category O has finite-dimensional weight spaces.
- Each module in category O is a Noetherian module.
- O is an abelian category
- O is closed to submodules, quotients and finite direct sums
- Objects in O are
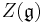 -finite, i.e. if
-finite, i.e. if  is an object and
is an object and 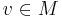 , then the subspace
, then the subspace 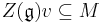 generated by
generated by  under the action of the center of the universal enveloping algebra, is finite-dimensional.
under the action of the center of the universal enveloping algebra, is finite-dimensional.
Examples
- All finite-dimensional
 -modules and their
-modules and their  -homomorphisms are in category O.
-homomorphisms are in category O. - Verma modules and generalized Verma modules and their
 -homomorphisms) are in category O.
-homomorphisms) are in category O.
See also
References
- Humphreys, James E. (2008), Representations of semisimple Lie algebras in the BGG category O, AMS, ISBN 978-0821846780, http://www.math.umass.edu/~jeh/bgg/main.pdf